INTRODUCCIÓN
Los juicios probabilísticos son parte del proceso de toma de decisiones porque la incertidumbre se encuentra presente en el proceso de decisión. El primer paso es el planteamiento general de cuál es la decisión que hay que tomar. Este planteamiento de la decisión determina las alternativas que se generan, lo que da lugar a resultados completamente diferentes. Por ejemplo, Luisa tiene 50 años no encuentra trabajo y tiene que decidir qué hacer: ¿cuál será la mejor forma de lograr un buen trabajo? Son alternativas centradas en aspectos económicos. Pero si, por el contrario: ¿qué pude podría ampliar su formación? ¿Pido ayuda a mi hermana para que me enchufe en una de las subcontratas que trabajan para su empresa? ¿Atraco un banco? Las alternativas serán diferentes. Esto mismo ocurre en decisiones políticas o sociales. Las alternativas generadas, la decisión, será completamente distinta según el tipo de preguntas que se haga el individuo.
Este planteamiento general está determinado por las metas de la persona. Los sujetos con metas a corto plazo o a largo plazo decidirán de forma diferente. Una persona que desea trabajar los dos meses de verano para ganar dinero e invertir en sus estudios futuros, puede elegir un empleo de muchas horas (aunque sea ilegal) y con mucha dedicación, y con un buen sueldo. Sin embargo, con metas a largo plazo, elegirá empleos que le permitan mantener calidad de vida, y ganar algo menos de salario.
Ante una decisión importante (deliberada y consciente) el siguiente paso sería la generación de las alternativas u opciones, sin desechar a priori ninguna de ellas. Serán diferentes en función del conocimiento y de los valores de la persona, así como de los factores socioculturales. Normalmente discriminar entre alternativas está determinado por la accesibilidad de la información, al decidir entre varios productos. Se tiende a tener en cuenta la información presentada y sólo en la forma que se presenta, ignorando a la vez datos que han de inferirse, transformarse o recuperarse de la memoria. P. ej. Al comprar un coche en función de la publicidad evaluamos las características más salientes, atendemos a los accesorios, diseño o detalle que el fabricante ha merecido hacer hincapié.
Una vez generado un número suficiente de alternativas, se evalúan con el fin de elegir la mejor. En la compra del coche pocas personas evalúan la fiabilidad, el consumo, o la seguridad. Una decisión correcta debería tener en cuenta tanto la probabilidad de que la característica se de (la tasa de fiabilidad de la marca elegida), como las consecuencias, que equivaldrían al valor o a la importancia que la persona da a esta característica.
Las estimaciones de la probabilidad se encuentran determinadas por el uso de heurísticos concretos y éstos a su vez influyen sobre la elección final de la opción. P. ej., las personas que sobreestiman la probabilidad de ocurrencia de una enfermedad grave por el impacto de una noticia. Este aumento de la probabilidad percibida producido por el heurístico de accesibilidad puede llevar a tomar decisiones sobre aplicar tratamiento o vacunación no siempre indicado. Estas sobreestimaciones de las probabilidades ocurren con las alternativas más deseables, y la subestimación con las menos. Esta tendencia es conocida como Principio de Pollyanna (protagonista de novela que siempre tenía alguna razón para ser feliz). Se da igualmente en los concursos o juegos de lotería en los que las personas que juegan sobreestimas las posibilidades de ganar el premio. También pueden darse otros sesgos, como el exceso de confianza en el juicio emitido o el sesgo retrospectivo consistente en la creencia, una vez conocido el resultado final, de que las cosas no podían suceder de distinta forma y que ya lo habíamos predicho.
En relación con la evaluación de las consecuencias de los resultados, es habitual conceptualizarlas en términos de ganancias o pérdidas. Es frecuente estudiar la toma de decisiones en los juegos de azar con situaciones de elección entre dos apuestas. Se ha tratado de investigar con los de elección bajo riesgo con un solo atributo en cada alternativa (ganancia o pérdida económica tras la ocurrencia o no del suceso); cuando es un tanto más compleja y cada alternativa muestra una serie de atributos, y requieren tanto de experto en el tema sobre el que se trata como de experto en el análisis de la decisión; y en otros casos se evalúa simultáneamente las probabilidades y las consecuencias porque éstas afectan a toda la población (análisis de campañas de vacunación contra enfermedades de baja prevalencia, pero cuyas consecuencias son graves que no permiten correr riesgos). En otros casos, la persona realiza una elección bajo incertidumbre evaluando expectativas y sus consecuencias. Las alternativas tienen cualidad para el individuo (beneficiosa o no) y una importancia determinada (según el grado de beneficio o perjuicio) que son diferentes para cada persona y que también varían en la misma en distintas situaciones (intraindividual).
TEORÍA NORMATIVA DE LA DECISIÓN
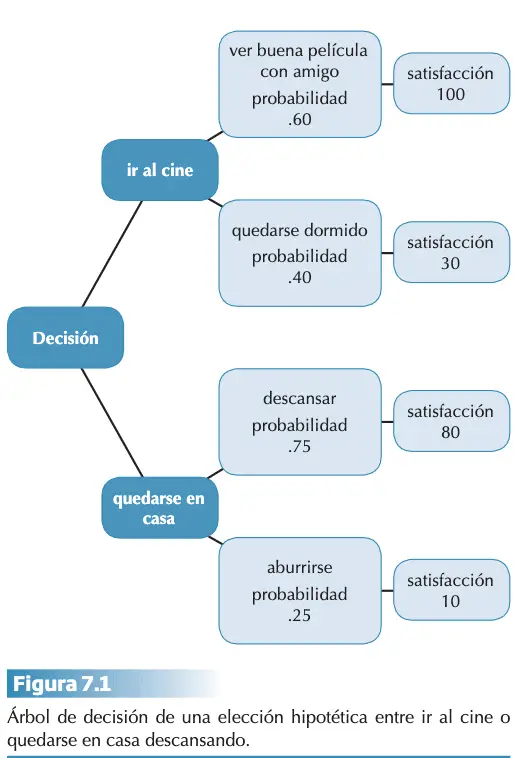
Una decisión es una respuesta a una situación en la que existe más de un curso posible de acción (opción o alternativa de elección). Suele basarse en las expectativas que tenemos sobre la ocurrencia de futuros acontecimientos y en la evaluación de las consecuencias de dichos acontecimientos en función de nuestras metas y valores. Imaginemos que llegamos de una jornada de trabajo agotados y nos invita un amigo a ir al cine. Ante tal situación se ha de elegir el quedarse en casa descansando o ir a ver la peli en buena compañía, pero con el riesgo de dormirnos en la misma. Los cursos de acción serían ir al cine o quedarnos en casa. Por cada una de esas opciones tenemos unas expectativas de lo que puede suceder. A la vez tenemos unas expectativas de lo que puede ocurrir: Desconocemos la probabilidad de ocurrencia de estos acontecimientos, pero podemos estimar su probabilidad y así evaluaremos sus consecuencias. En una escala de satisfacción entre 0 y 100 (ver figura 7.1).
En el diagrama en forma de árbol de decisión de la situación estamos combinando las propias expectativas con los intereses y los deseos personales. El árbol de decisión no proporciona una solución, pero sí la representación de las expectativas sobre la ocurrencia de los hechos futuros y de la evaluación de sus consecuencias. Ello permite visualizar gráficamente cuál es la alternativa que brinda una mayor satisfacción y su expectativa según nuestros criterios.
En la toma de decisiones se suelen diferenciar tres situaciones relacionadas con las expectativas:
- Aquellas en las que se conocen las probabilidades (comprar un billete de lotería).
- En las que se desconocen las probabilidades y éstas se pueden estimar (seguir trabajando en la empresa familiar o poner negocio propio).
- Situaciones en las que hay certeza sobre las opciones y sólo se ha de elegir entre las mismas (pedir carne o pescado en el restaurante) La certeza indica que no hay dudas sobre los acontecimientos futuros y la decisión se toma bajo este supuesto.
Las expectativas se definen como el grado de creencia o probabilidad de que ocurra un acontecimiento concreto. Generadas éstas, se evalúan sus consecuencias asociadas en función de criterios personales. Se considera que la decisión se toma en un contexto de riesgo cuando se conocen las probabilidades, en un contexto de incertidumbre cuando éstas se estiman y en uno de certidumbre cuando se conoce con seguridad la ocurrencia.
La teoría normativa asume que cuando decidimos, lo hacemos eligiendo aquello que tiene el máximo valor en los resultados que se esperan obtener. Unos matemáticos del XVII y XVIII (Bernoulli) consideraron estudiar la probabilidad y la toma de decisiones en los juegos de azar como pauta de comportamiento óptima. El objetivo era encontrar la forma de cuantificar el valor de una apuesta en los juegos o en decisiones bajo condiciones de riesgo. Bajo este supuesto se denominaron Modelos del valor esperado coincidiendo este valor con la esperanza matemática el juego.
El Valor esperado de una alternativa es la suma del producto de cada valor por su probabilidad de ocurrencia y la mejor elección será aquella que obtenga el máximo valor esperado.

La alternativa 1 es la mejor porque tiene un valor esperado de 900 euros frente a 404 de la 2ª. Esta cantidad es promedio ponderado de los resultados que se esperan ocurran en el futuro. Se pondera cada resultado posible con respecto a la frecuencia con que se espera. También se puede obtener a partir de estimaciones subjetivas, y es el valor esperado la representación de las creencias personales sobre la ocurrencia del posible resultado.
Según la teoría del valor esperado los sujetos buscan maximizar sus ganancias y elegirán la opción 1. No obstante, no todos se ajustan a la elección y prefieren la opción 2, en la que se gana menos, pero se gana siempre. Ello hizo que el “valor esperado” fuera sustituido por el concepto de la utilidad esperada, entendida como el grado en que las consecuencias de una opción alcanzan las metas personales en una situación determinada.
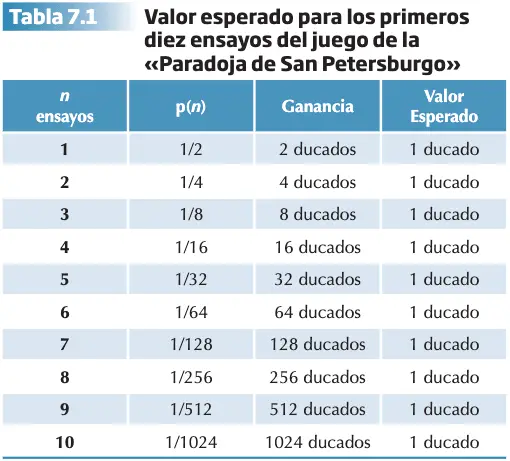
La primera objeción importante a este criterio fue en el S.XVIII y se atribuye a Nicolás Bernoulli, aunque fue su primo Daniel Bernoulli el que desarrolló y lo publicó como “Paradoja de San Petersburgo”. En la paradoja de San Petersburgo se planteaba un juego de azar entre dos jugadores de la siguiente forma. El jugador A plantea la regla del juego y el jugador B tiene que decidir cuánto dinero está dispuesto a pagar por participar en dicho juego. La regla consiste en que el jugador A lanzará una moneda hasta que caiga en el lado de la cara y el número de lanzamientos necesarios para conseguir obtener el lado de la cara determinará la cuantía del premio. Si el jugador A lanza una moneda y sale cara en la primera tirada, entonces pagará 2 ducados al jugador B y termina el juego. Si la primera cara de la moneda sale en la segunda tirada, entonces pagará 4 ducados, si sale en la tercera tirada, pagará 8 ducados y así sucesivamente. La pregunta que se plantea en la paradoja es la siguiente: ¿Cuánto pagaría el jugador B al jugador A por participar en este juego?
Según el criterio del valor esperado, el jugador B debería participar en el juego si el valor esperado es mayor que la suma exigida para entrar a jugar y rechazar la propuesta cuando ésta sea menor. Para calcular el valor esperado total del juego se suman todos los valores esperados en cada lanzamiento (1+1+1+1+1+…+…=?), dando como resultado un número infinito de “ducados”. La paradoja surge porque con un valor infinito se debería apostar cualquier cantidad de dinero. Al señor B le interesa que salga cara lo más tarde posible. Los resultados evidenciaron que generalmente no están dispuestas a apostar más de 20 monedas por participar. Pone de manifiesto que no es realista asumir que B espere poder jugar durante tiempo ilimitado para obtener número infinito de monedas a cualquier precio.
Para resolverlo, Daniel Bernoulli (1738) propuso la noción de utilidad esperada como valoración subjetiva de las posibles consecuencias monetarias del juego. Es en función de la riqueza de cada individuo y está en relación inversa a su nivel de riqueza. Ganar o perder 200 euros no es lo mismo para un rico que para un pobre, y cuánto más dinero se tenga menos se valorará dicha ganancia o pérdida. El autor también comenta de utilidad marginal decreciente al señalar que la función de utilidad es siempre creciente, pero crece cada vez más despacio. Es necesario diferenciar entre el valor esperado (cantidad objetiva) y la utilidad esperada que depende de las circunstancias subjetivas de cada uno. En la paradoja descrita los individuos están dispuestos a pagar distintas cantidades por participar en el juego según su criterio, aunque el valor esperado sea infinito. Esta distinción permite analizar la toma de decisiones bajo riesgo considerando las valoraciones subjetivas que hacemos. Daniel Bernoulli cuenta con el reconocimiento de haber sentado las bases de la moderna teoría de la decisión al lograr demostrar que el valor del dinero no es el mismo para todos y que las personas lo valoran en proporción a la utilidad que pueden obtener de él.
Teoría de la utilidad esperada
El concepto de utilidad esperada de Daniel Bernoulli fue retomado por Neumann y el economista Oskar Morgenstern (1944) . La teoría de la utilidad esperada de Neumann y Morgenstern ha sido el modelo estándar de la decisión individual en situaciones de riesgo. Esta teoría del ámbito de la economía está interesada en “qué” deciden las personas más que en “cómo” deciden. Su interés se centra en el análisis de la relación entre aquello que se decide y los valores personales que le han llevado a ella. El resultado del análisis permite entender los actos de elección como las actitudes que tiene una persona hacia el riesgo.
Los autores proponen unos axiomas que garantizan la coherencia en el proceso de toma de decisiones. Se necesita una escala de preferencias con la que poder evaluar las opciones. La noción de utilidad es la escala de preferencias con mayor aceptación de los modelos normativos. Con esta se está asumiendo que las metas u objetivos de las personas se expresan en sus preferencias, buscando resultados acordes con los valores que se tienen.
Se asume que los atributos de una opción son independientes y que cada uno tiene un peso o importancia. Implica ello que cada uno tiene una utilidad que indica el grado en que esa propiedad contribuye a alcanzar las metas y objetivos. Las personas conocen su entorno, son capaces de ordenar las alternativas según el criterio de utilidad y eligen la de mayor proceso de maximización. La decisión óptima será aquella que refleje sus preferencias.
Como modelo normativo, la teoría de la utilidad esperada también presenta las siguientes ventajas:
- La consideración de toda la información disponible sobre las diferentes opciones.
- La comparación entre cualquier par de opciones dado que comparten una misma escala de preferencias.
- El establecimiento de una estructura de preferencias coherente a partir de la determinación de la utilidad de cada opción.
Los axiomas de la teoría de la utilidad esperada
El trabajo de van Neumann y Morgenstern es una aproximación metodológica al estudio de la toma de decisiones bajo riesgo que ofrece un conjunto de axiomas para poder construir una escala de utilidades en la que la representación de los valores de las consecuencias se ajuste a una concepción ordinal de la utilidad. Los axiomas son principios fundamentales e indemostrables sobre los que se construye una teoría. Son proposiciones claras y evidentes que se admiten sin demostración, pero pueden no serlo. A veces estos axiomas pueden no ser necesariamente evidentes, pero su expresión lógica se utiliza para la deducción y así poder generar conceptos a partir de ellos.
Savage (1954) generalizó la teoría de la utilidad esperada para permitir la inclusión de las probabilidades subjetivas basadas en las creencias propias u opiniones sobre probabilidad de los hechos. Edwards (1954) denomina a esta ampliación “el modelo de la utilidad subjetiva esperada” en un artículo que fue el primer intento de la psicología por acercarse a este dominio. Sin embargo, no es habitual hacer una distinción porque los axiomas y teoremas sistematizados de Savage cumple las leyes de la teoría de la utilidad esperada y las probabilidades subjetivas que contempla, cumplen las leyes de la probabilidad.
AXIOMAS DE LA TEORÍA DE LA UTILIDAD ESPERADA
- Axioma de completitud u ordenamiento completo: (A > B); (B > A); (A ? B). A y B son alternativas del conjunto S, entonces siempre es cierto uno y solo uno de los siguientes enunciados:
- A se prefiere a B
- B se prefiere a A
- Se prefieren las dos, y por tanto, son indiferentes ante un conjunto de alternativas, las personas pueden ordenarlas según las preferencias asumiendo que es posible ser indiferente (A ? B).
Con este axioma damos por supuesto que, ante un conjunto de alternativas, las personas pueden ordenarlas según sus preferencias (de más a menos preferidas). P. ej., Supongamos que han convocado elecciones y tenemos que elegir entre votar PP o VOX, según este axioma tendríamos 3 opciones: Votar PP, votar Vox o nos da igual votar PP o VOX.
- Axioma de transitividad: Si (A > B) y (B > C), entonces (A > C). Este axioma permite relacionar el orden de preferencias entre 2 alternativas a través de una tercera en común. Siguiendo el ejemplo de las elecciones si el votante prefiere votar a VOX antes que al PP, y a su vez prefiere votar al PP antes que votar Cs, según este axioma se debería votar a VOX.
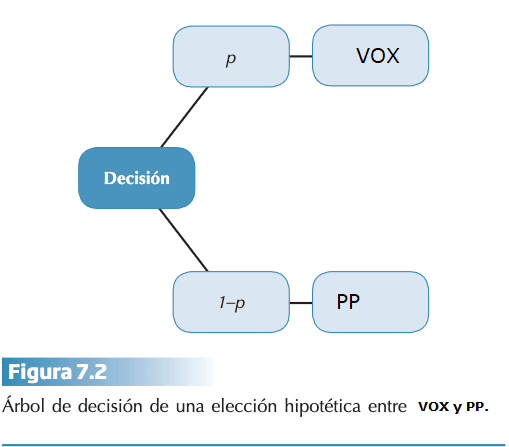
- Axioma de cierre: si A y B son alternativas de un conjunto S, entonces ApB también lo son. La expresión ApB del axioma de cierre indica que ambas probabilidades (p y 1-p) también pertenecen al mismo conjunto S. Este axioma expresa una relación de pertenencia. Enuncia la capacidad de las personas para conceptualizar las probabilidades asociadas con las alternativas. Si A y B son alternativas de un conjunto S, entonces la probabilidad de la alternativa A (p) y la probabilidad de la alternativa B (p-1) también forman parte de ese conjunto. En el ejemplo de las elecciones tanto VOX (P) como el PP (P-1) forman parte del mismo conjunto (neoliberalismo).
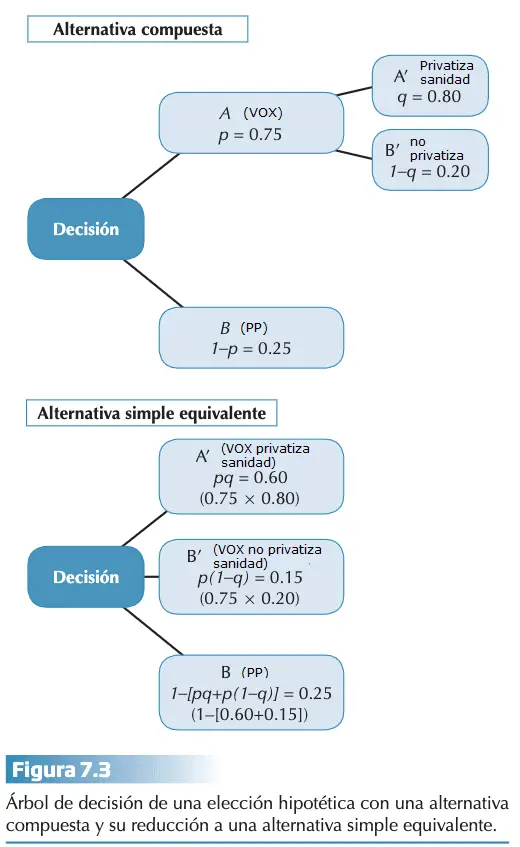
- Axioma de reductibilidad: [(ApB)qA´]?(ApqB)]. Este axioma introduce la distribución de probabilidades entre alternativas para poder descomponer una alternativa compuesta en una simple. Alguna de sus consecuencias es también una alternativa. Las reglas de la probabilidad permiten reducir toda alternativa compuesta a una simple que sea equivalente. Supongamos que en el ejemplo de las elecciones existe una probabilidad del 75% de votar VOX (alternativa A) y de un 25% de votar PP (alternativa B). A su vez la probabilidad de que VOX privatice la sanidad pública es del 80%, y un 20% de que no lo haga.
- Axioma de consistencia: (A > B) si y solo si A > (ApB) > B. Este axioma es básico y nos indica que si la alternativa A se prefiere a B, entonces la A se prefiere siempre que se presente con cierta probabilidad. Siguiendo con las elecciones, si preferimos VOX al PP (A>B), entonces también preferimos cualquier alternativa que permita que VOX tenga poder, en este caso se preferiría la opción VOX y PP, antes que PP en solitario.
- Axioma de independencia: (A > B) si y solo si (ApC) > (BpC). El orden de preferencias entre dos alternativas simples no cambia por la adición de una nueva alternativa. P. ej., si preferimos VOX al PP (A > B) como opción política, entonces deberíamos preferir una alternativa compuesta por VOX y Cs (ApC) frente a otra compuesta por el PP y Cs. (BpC).
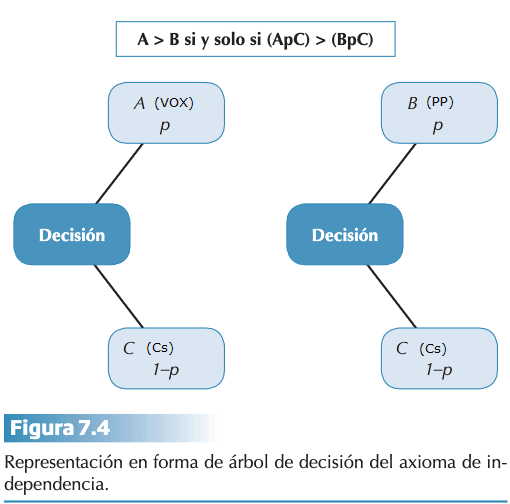
- Axioma de continuidad: Si (A>B>C), entonces existe una probabilidad p tal que B ? (ApC). Este axioma es importante para la construcción de la escala de utilidad porque asume que habrá un valor entre 0 y 1 que permite que la persona sea indiferente. Siguiendo con el ejemplo de las elecciones si VOX (A) es preferido al PP (B) y el PP (B) es preferido a Cs (C), entonces siempre es posible encontrar una probabilidad p para que la alternativa PP sea equivalente a la combinación de la probabilidad p de VOX con la probabilidad 1–p de Cs (VOX p Cs). Con esto se asegura que no haya una alternativa mejor o peor a las otras y se puede localizar en la escala la opción B entre A y C.
Cuando se cumplen estos axiomas la función de utilidad establece lo siguiente:
- (x) se prefiere a (y) si y solo si la utilidad de (x) es mayor o igual a (y). [U(x)?U(y)]
- La utilidad de una alternativa es igual a la utilidad de cada resultado ponderada por su probabilidad: [U (x1p1….xnpn) = p1u(x1) + p2u(x2) + …….. pnu(xn)]
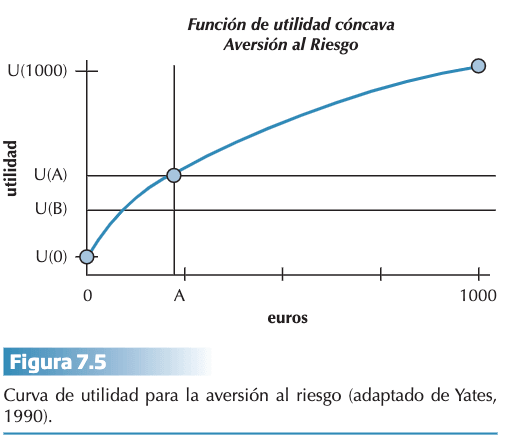
A partir de estas dos propiedades se puede construir la curva de la función de utilidad. Supongamos que tenemos que elegir entre 2 alternativas:
- OPCIÓN A: una ganancia segura de 240 euros.
- OPCIÓN B: un 25% de probabilidades de ganar 1000 euros y un 75 % de ganar 0 euros.
Si eligen la opción A, sabemos que han asignado una utilidad mayor al valor esperado de 240 euros que al valor esperado de 250 euros, lo que es compatible con una persona con aversión al riesgo. Calculamos:
U(B)=0.25 U (1000€) + 0.75 U(0€) = 250€
U(A)= U(240€)
U(A)>U(B)
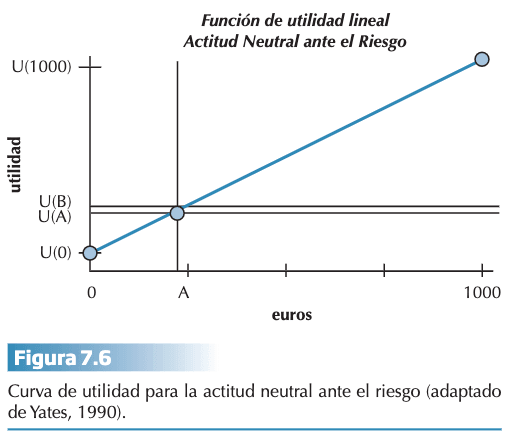
Si la utilidad esperada fuera proporcional a la cantidad del valor esperado, sería lineal y representaría una actitud neutral hacia el riesgo. La utilidad B, U(B) sería = U(A).
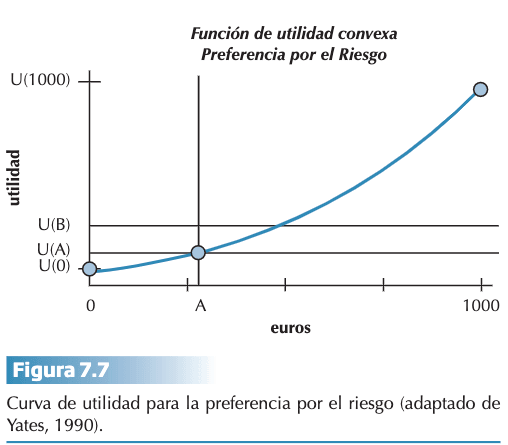
También encontramos personas que presentan preferencia por el riesgo al elegir situaciones con mayor riesgo por una mayor cantidad de dinero de menor riesgo y menor cantidad de dinero. Supongamos las opciones son otras:
- OPCIÓN A: una ganancia segura de 260 euros.
- OPCIÓN B: un 25% de probabilidades de ganar 1000 euros y un 75 % de ganar 0 euros.
U(B) 0.25 U(1000€) + 0,75 U(0€) = 250 euros
U(A) = U(260€)
U(B)>U(A)
Esta utilidad describe las preferencias de un sujeto y los axiomas imponen las restricciones sobre sus posibles relaciones, aunque no determinen cuáles son estas transferencias. Esta teoría proponía que para ser racionales en la toma de decisiones no hacía falta compartir la misma función de utilidad, sino que bastaba con ajustarse a los mismos axiomas normativos en esa búsqueda por alcanzar la máxima utilidad esperada que había sido definida individualmente.
Objeciones a la teoría de la utilidad esperada
Los axiomas anteriores fueron objeto de críticas entre las que destacan las conocidas como paradojas de Allais (1953) y Ellsberg (1961). Estas paradojas indicaban como se podían violar algunas de las restricciones impuestas, cuestionando así el concepto de racionalidad subyacente de la teoría.
La paradoja formulada por Allais se centra en la violación del axioma de independencia. Si una alternativa A se prefiere a B, entonces cualquier combinación de A y C con una probabilidad determinada debe ser preferida a otra combinación de B con C con la misma probabilidad. Allais describió dos situaciones:
Primera situación:
Alternativa A: ganar 1 millón de euros con la probabilidad 1 (con total certeza).
Alternativa B: ganar 2,5 millones con la probabilidad de 0,10. ganar 1 millón con la probabilidad de 0,89, o ganar 0 euros con probabilidad de 0,01.
En esta primera la mayoría opta por la alternativa A en la que se gana 1 millón con certeza. Para hacer el cálculo de la utilidad esperada entre ambas alternativas se considera la ganancia de 1 millón eliminando la probabilidad de la misma de la alternativa B y conservando la probabilidad restante en la alternativa A (1 – 0,89=0,11). Las alternativas quedarían de la siguiente forma:
Alternativa A: ganar 1 millón con probabilidad de 0,11
Alternativa B: ganar 2,5 millones con probabilidad de 0,10 y ganar 0 euros con probabilidad de 0,01
Elegir la opción A implica que la utilidad U(A) 0,11 es mayor que la utilidad de la alternativa B , donde U(B) 0,25.
U(A)0.11>U(B)0.25
U(A)=0.11 U(1 millón)=0,11
U(B)=0.10 U(2.5 millones)+0,01U(0€)=0.25
La paradoja se plantea cuando se presenta la segunda situación en la que las dos alternativas comparten una ganancia de 0 euros.
Segunda situación:
Alternativa C: ganar 1 millón con la probabilidad de 0.11; ganar 0 euros con probabilidad de 0.89
Alternativa D: ganar 2,5 millones con probabilidad de 0.10 ganar 0 euros con probabilidad de 0.90
Considerando la ganancia común de 0 euros en C y conservando la probabilidad restante en la alternativa D (0.90 – 0.89 = 0.01) la situación sería:
Alternativa C: ganar 1 millón con probabilidad de 0.11.
Alternativa D: ganar 2.5 millones con probabilidad de 0.10 ganar 0 euros con probabilidad de 0.01.
La mayoría de las personas prefieren la alternativa D inicialmente. Implica que U(C) 0.11 es menor que la utilidad de la alternativa D, U(D) 0,25.
U(C) 0.11 < U(D) 0.25
U(C) = 0.11 U(1 millón)= 0.11
U(D) = 0.1 o U(2.5 millones)+ 0.01 U(0 €) = 0.25

Savage (1954) hace un análisis de la paradoja de Allais ampliando el axioma de independencia con el principio denominado aspecto cierto (sure-thing). Este principio afirma que, si dos alternativas comparten un resultado concreto, la preferencia será independiente del valor de este resultado común. Las personas descartan el resultado seguro y basarán su elección en los posibles resultados diferentes entre alternativas. Como se puede ver, la alternativa A se ha colocado en todas las casillas porque ofrece una ganancia segura en todos los rangos de probabilidad. Al comparar las casillas entre las alternativas A y B encontramos que el aspecto seguro se encuentra en la ganancia de 1 millón€ con una probabilidad 0.89 (tercera casilla). Por tanto, este resultado se descartará y la decisión entre las alternativas A y B se centrará en elegir entre la probabilidad 0.01 de ganar 1 millón€ ó 0€ y la probabilidad 0.10 de ganar 1 millón€ ó 2.5 millones€.
Para las alternativas C y D, el aspecto seguro se encuentra en la casilla de la ganancia de 0€ con una probabilidad de 0.89. La ganancia de 0€ también se ha colocado en la casilla con una probabilidad de 0.01 para completar la probabilidad de 0.90 de la alternativa D (0.89 + 0.01 = 0.90). En la alternativa C, la ganancia de 1 millón€ con probabilidad 0.11 se ha colocado en las casillas con probabilidades de 0.01 y 0.1 O (0.01 + 0.1 O = 0.11). Cuando se descarta el aspecto cierto entre las alternativas C y D se puede comprobar que la decisión sigue siendo elegir entre la probabilidad 0.01 de ganar 1 millón€ ó 0€ y la probabilidad 0.1 O de ganar 1 millón€ ó 2.5 millones€.
La elección de las alternativas A y D contradice la coherencia del orden de preferencias. Es opuesta dependiendo de cómo se presente el problema, lo que contradice el principio descrito por la teoría de la utilidad. En la primera situación, se prefiere la opción A con ganancia segura menor que en B en la que existe una probabilidad aún pequeña de quedarse sin nada. En la segunda situación, la pequeña diferencia existente entre probabilidades de las dos alternativas queda compensada por la gran diferencia entre ganancias.
La segunda paradoja planteada por Ellsberg (1961) se basa en el concepto de ambigüedad . Se ex- traen bolas de colores. 90 bolas: 30 rojas, 60 negras y amarillas en proporción desconocida. La extracción al azar supone ganancia distinta en función del color. Se presentan dos situaciones:

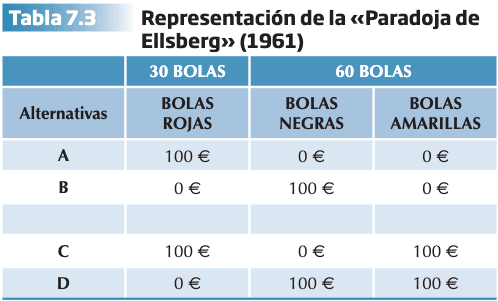
La mayoría prefiere la opción A en la primera situación y la D en la segunda. La elección indica la preferencia por ganancias con probabilidades conocidas, evitando la ambigüedad de la probabilidad de obtener una bola negra o amarilla. También violan el axioma de independencia. El aspecto cierto entre las alternativas se encuentra en las bolas amarillas.
Por tanto, la teoría de la utilidad esperada se ha descartado como modelo normativo válido de la toma de decisiones. Se puede considerar que es una guía prescriptiva adecuada o un buen criterio para el hombre racional, pero no un modelo descriptivo de decisiones. Analiza cómo debería de ser una decisión correcta, para una correcta planificación, inversión o estrategias políticas, pero no es buena descripción de las elecciones de las personas en su vida diaria.
TEORÍAS DESCRIPTIVAS DE LA DECISIÓN
Las personas asignan probabilidades subjetivas tal y como se establece sino en base a atajos cognitivos, aunque estos sean erróneos. Pronto la evidencia empírica y los resultados experimentales mostraron que los axiomas se violaban repetidamente. Se expone un ejemplo de que no se cumple el axioma de la transitividad donde A >B y B > C, entonces se prefiere A sobre C. Según Tversky se da dentro de un entorno cotidiano la decisión no correcta: Estudiante que quiere completar sus estudios y debe elegir entre psicología, sociología y antropología.
Descubriendo que ha de inscribirse rápidamente por pocas plazas considera inicialmente su preferencia hacia la psicología con mayor calidad de enseñanza. Mientras espera piensa que su mayor interés es la sociología y podría obtener calificación mayor. Parece mejor optar por esta alternativa, pero sigue pensando y considera que el curso de antropología tiene calidad mayor, con posibilidad de calificación mejor, por lo que definitivamente opta por esta. Aún así sigue pensando en su elección inicial…
Esta descripción de la violación de la transitividad en las elecciones se presenta a menudo incluso en casos simples como el expuesto. Slovic y Tversky (1974) encontraron que los sujetos eran inconsistentes en sus preferencias ante situaciones de elección semejantes a la conocida paradoja de Allais:

Las cantidades de dinero son las mismas en las 2 situaciones, pero las probabilidades de la situación 2 se han dividido. Según la utilidad esperada, aquellos que elijan la alternativa A deberían elegir la C, y si eligen la B, luego debían optar por la D. La mayoría (78%) prefería la alternativa A en la situación 1, al elegir esta opción mostraban aversión al riesgo porque preferían ganar 30 $ sin riesgos que ganar más con un riesgo de 0,20 o no ganar nada. En la segunda situación la mayoría (58%) elegían la alternativa D donde mostraban que preferían ganar 45 $ con un riesgo de 0,80 que 30 $ con un riesgo de 0,75, demostrando lo indicado por Allais con el axioma de independencia de la teoría de la utilidad esperada. Lo denominaron “efecto de la certeza” porque la reducción de una ganancia segura a una ganancia con una probabilidad de 0,25 tiene mayor impacto, que la correspondiente reducción de una probabilidad de 0,80 a 0,20.
Otros resultados, también discrepantes con la teoría de la utilidad esperada muestran la violación del principio de invarianza. Este es un supuesto básico implícito para la coherencia sustentada por los axiomas. Establece que la relación entre las preferencias no debe depender de la descripción de las alternativas o del procedimiento utilizado para hacer la elección. A continuación vamos a ver los resultados de dos estudios que muestran cómo las personas muestran una actitud diferente ante el riesgo según se presenten los problemas en términos de ganancias o pérdidas (Tversky y Kahneman, 1981 ). Las situaciones de elección que se presentaron a los sujetos fueron las siguientes:


En términos de la utilidad esperada, ambos problemas son idénticos. Las dos situaciones plantean una elección entre 400$ seguros o 500 $ y 300 $ con una probabilidad de 0,50. Los resultados mostraron que la mayoría (72%) elegía la alternativa A en la situación 1 y la alternativa D (64%), en la situación 2. El valor esperado es igual, pero se encuentra que cuando el problema se formula en términos de ganancias, los sujetos muestran actitud aversiva al riesgo. Y cuando se presenta en términos de pérdidas, se muestra una preferencia por el riesgo. Este efecto es conocido como el efecto del marco (framing effect) o de la inversión de las preferencias sin limitarse a aspectos monetarios.
En otro estudio de Tversky y Kahneman (1981), se planteaba la elección entre dos programas saniarios:

Los programas A y B tienen el mismo valor esperado (salvar 200 frente a 400) y los programas C y D son idénticos a los programas A y B, (400 muertes frente a salvar 200 vidas). En la 1ª situación la mayoría (72%) elegía opción A, mostrando la aversión al riesgo y el efecto de certeza. En la 2ª situación, la mayoría (78%) eligieron el D, mostrando una preferencia por el riesgo y evitando una pérdida segura. Un claro ejemplo de la inversión de las preferencias (framing effect) para las ganancias y las pérdidas puesto que las dos situaciones son idénticas y de la violación del principio de invarianza. Este nos recuerda que las elecciones no deberían cambiar en función de la descripción de la situación o de la formulación de los problemas, siempre que contengan la misma información.
En otro estudio de Tversky, Sattah y Slovic (1988) relacionado también con la violación el principio de invarianza. Las preferencias manifestadas no deberían cambiar si cambia el método por el cual se obtienen. Siguiendo este principio, los autores partieron del supuesto de que, si los sujetos prefieren una determinada alternativa en una tarea de elección, entonces también deberían preferir esa misma alternativa cuando en otra tarea se les pide asignarle un coste. En este estudio se describía la siguiente situación:

A un grupo se le pedía elegir entre los dos programas y la mayoría (67%) opto por el programa X. Preferían salvar 70 vidas que ahorrar 43 millones. A un segundo grupo se le presentaba lo mismo, pero sin indicar costo del programa Y (12 millones) y debían estimar el coste que considerasen necesario para que las dos alternativas fuesen atractivas por igual.
El coste de Y debería ser menor que en el programa X pues morían más. Si se tiene en cuenta solo el coste, será preferible la alternativa más barata y podemos inferir qué prefieren los sujetos a partir de la cantidad asignada para igualarlas. Si establecen el coste superior a 12 millones significa que prefieren el programa X porque la diferencia entre ambos se reduce. Si lo establecen menor, prefieren el Y dado que la diferencia se incrementa. Cuando se pedía este tipo de respuesta se prefería el Y en su mayoría (96%). Los autores lo explican por la importancia relativa a los atributos (vidas salvadas) pero pierden peso cuando se trata de tasar o poner precio. Concluyen este estudio sugiriendo que las personas mostrarán su apoyo a una iniciativa pública de forma diferente según se pregunte en las encuestas por sus preferencias o por su opinión sobre la cuantía de sus costes.
Esta violación del principio de invarianza también se presenta cuando la persona toma una decisión de elección de una alternativa y cambia por la decisión de rechazarla. En una decisión binaria no debería influir la elección o el rechazo: si A se prefiere a B, entonces se rechazará B frente a A. Shafir (1993) encontró que los atributos positivos son más importantes cuando se trata de una elección y los negativos cobran importancia cuando se trata de un rechazo. En este estudio se pedía a un primer grupo de sujetos que tomaran la decisión de concederle la custodia a uno de los dos progenitores y a un segundo grupo la decisión de denegarla. Para poder tomar la decisión se presentaban datos relacionados con el estatus económico, social y emocional de ambos progenitores.
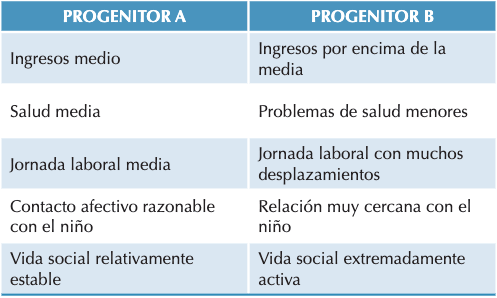
Como se puede apreciar, la información correspondiente al progenitor A es una información media, sin atributos que destaquen en lo positivo o negativo. Sin embargo, en la información sobre el progenitor B hay una combinación de atributos que sobresalen en ambos sentidos. Los resultados mostraron que la mayoría de los sujetos elegían tanto otorgarle la custodia como denegarle su concesión al progenitor B. Esta discrepancia muestra cómo dos tareas que en principio son lógicamente equivalentes dan lugar a dos elecciones distintas.
Las personas no atienden únicamente a la utilidad de los componentes de cada alternativa para decidir sobre la utilidad global. Prefieren la alternativa cierta cuando se ofrece ganancia y prefieren arriesgarse cuando se trata de pérdidas de la misma magnitud. No siguen leyes lógicas de transitividad o independencia, en muchas ocasiones las preferencias dependen de alguna variable del contexto y de la tarea. Aún cuando parecen ajustarse a la lógica, no significa que traten de maximizar el valor o la utilidad de las alternativas. Por tanto, hay que considerar los aspectos subjetivos o propios de la persona.
Teoría de la Perspectiva
La teoría de la perspectiva de Kahneman y Tversky (1979, 1992) es una modificación de la teoría de la utilidad esperada basada en la descripción de las decisiones de los sujetos. Pretende remediar las deficiencias anteriores. Introduce dos conceptos nuevos: el valor y el peso de las alternativas. La Teoría de la perspectiva asume que el valor de una opción es el resultado de la suma del producto del valor asignado a cada resultado X por el peso otorgado a la probabilidad de obtener X.
V=w(p1)v(x1) + w(p2)v(x2)+………… w(pn)v(xn)
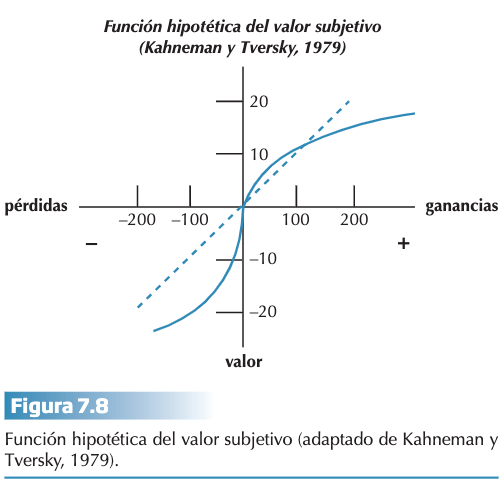
El concepto de utilidad se sustituye por el concepto de valor, que se define en términos de ganancias y pérdidas desde un punto de referencia y no absolutos. La función del valor tiene forma de “S” y es asimétrica, donde el valor que se atribuye a cada nueva unidad es cada vez menor (pierde pendiente) y esto explica que en términos de ganancias se prefiera una segura a otra mayor pero solo probable (aversión al riesgo) y que en términos de pérdidas se prefiera asumir el riesgo de una pérdida mayor en lugar de evitar la pérdida menor pero segura. La asimetría explica los resultados que muestran mayor sensibilidad al grado de desviación de un resultado con respecto a un punto de referencia que al resultado por sí solo (se observa mayor impacto en el ámbito de las pérdidas que en el de las ganancias).
Si nos fijamos en la figura 7.8, vemos la forma de S de la función del valor, que en el caso de las ganancias es cóncava y en caso de pérdidas es convexa. Además, el valor que se atribuye a cada nueva unidad es cada vez menor, de ahí que pierda pendiente. Esto explica que en términos de ganancia se prefiera ganancia segura a otra mayor pero probable (aversión al riesgo), y que en términos de pérdidas se prefiera asumir el riesgo a una pérdida mayor en lugar de evitar una pérdida menor pero segura (preferencia por el riesgo).
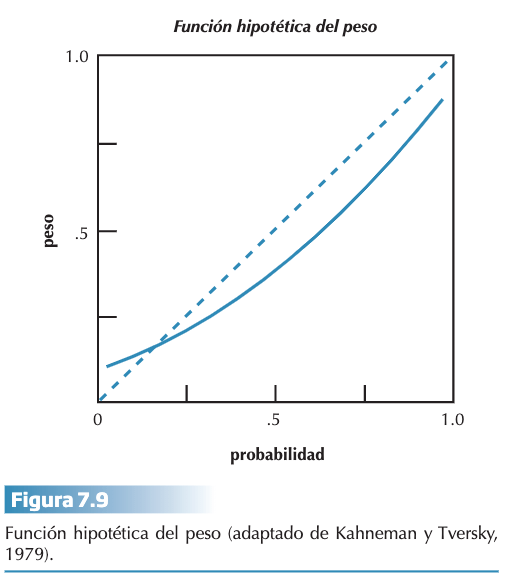
En relación con el tratamiento de las probabilidades de las alternativas, la teoría de la perspectiva considera que los sujetos en sus decisiones no ponderan las alternativas con sus probabilidades objetivas, sino que lo hacen con unas ponderaciones que denominan pesos decisorios. Como podemos ver en la Figura 7 .9, los pesos decisorios guardan una relación no lineal con las probabilidades objetivas: los pesos son mayores cuando las probabilidades son bajas (sobreestimación), van perdiendo pendiente y son menores a partir de los tramos centrales de las probabilidades (subestimación) y se recuperan cuando las probabilidades son altas (efecto de la certeza).
Las aportaciones principales señalan que la función del valor subjetivo es cóncava para ganancias y convexa para las pérdidas y su inclinación es mayor cerca del punto de referencia (sensibilidad a ganancias o pérdidas en mayor en la primera unidad +10 y -10). Se postulan que se subestiman las probabilidades moderadas y altas, y se sobreestiman las probabilidades pequeñas y la certeza.
En la Tabla 7.4. podemos ver el patrón habitual de las actitudes hacia el riesgo encontrado por Tversky y Kahneman (1992).
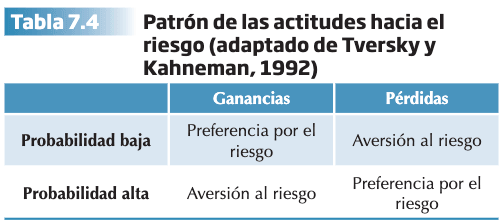
Se distinguen dos fases: “edición” revisión preliminar de las alternativas y “evaluación” que da lugar a la elección de la alternativa que haya obtenido el valor más alto.
La fase de “edición” organiza y reformula las alternativas para simplificar los siguientes procesos de evaluación y elección. Se aplican las operaciones:
- Codificación de los resultados en pérdidas y ganancias. Estos se definen en relación con un punto de referencia. Si corresponde con el estado del problema, las ganancias y pérdidas coinciden, pero este punto de referencia puede cambiar por la formulación del problema o expectativas de la persona.
- Combinación de las probabilidades asociadas a resultados idénticos. Permite simplificar el conjunto de alternativas: 200 euros con probabilidad de 0,25 más otros 200 euros con probabilidad de 0,25, puede reducirse a 200 euros con probabilidad de 0,50.
- Segregación de los componentes ciertos de los componentes con riesgo. Una alternativa de 300 euros con probabilidad de 0,80 y 200 euros con probabilidad de 0,20 se puede descomponer en una ganancia segura de 200 euros y una ganancia de 100 euros con probabilidad de 0,80. Al final serán 280 euros.
- Cancelación de los componentes compartidos por todas las alternativas. La opción común se cancela.
- Simplificación por el redondeo o por eliminación de las alternativas muy poco probables. 101 euros con probabilidad de 0,49 euros puede considerar como 100 con probabilidad de 0,50.
Editadas se pasa a la fase de “evaluación” que comprende la función del valor subjetivo y la función de la probabilidad ponderada de obtener un resultado. Las estimaciones del valor de una alternativa son cambios de riqueza o bienestar y no en estados finales. El valor es tratado como una función con dos aspectos: una posición inicial que sirve de punto de referencia y la magnitud del cambio desde ese punto de referencia. La teoría se basa en una ecuación básica que describe la forma en la que se combinan la probabilidad y el valor subjetivo para determinar el valor global de las alternativas. Puede aplicarse a elecciones que implican otros atributos como calidad de vida etc. y no sólo a cantidades de dinero. Lo único que precisa es que los resultados esperados sean codificados como ganancias o pérdidas en relación a un punto de referencia y que las pérdidas sean percibidas como más graves que las ganancias del mismo tamaño.
Teoría Portafolio (Coombs, 1969;1975)
Otros enfoques describen sencilla y naturalmente el proceso de elección entre alternativas centrados en la relación entre el valor esperado y el riesgo. Consideran dos aspectos: 1) la promesa de ganancia potencial de cierta cantidad, 2) el riesgo como posibilidad de sufrir una pérdida. Coombs (1969;1975) centra su interés en analizar el riesgo y su relación con el valor esperado, señalando que tomamos decisiones bajo riesgo adoptando compromiso entre maximizar el valor esperado y optimizar el riesgo. Sostiene que las personas tenemos niveles de riesgo diferente y que cada una elegiríamos la alternativa que más se aproxime a nuestro nivel de riesgo ideal.
La teoría Portafolio incluye el riesgo percibido de cada alternativa como determinante de la elección de las personas siendo en función de la probabilidad de perder y también de la cuantía de esa pérdida. Para cada nivel del valor esperado existe también un nivel óptimo: riesgo ideal, donde la persona elige la alternativa A frente a B poniendo de manifiesto que A se encuentra más cercana al riesgo ideal que B. Cuando presentan el mismo valor esperado la elección será función únicamente del riesgo. Los resultados experimentales de Coombs y Huang (1970) confirmaron que los sujetos elegían la alternativa con el mayor valor esperado cuando la diferencia entre los diferentes niveles de riesgos y el riesgo ideal era la misma. Encontraron que este nivel de riesgo ideal y persona no era el mínimo nivel de riesgo posible. Estas diferencias individuales no deberían considerarse como rasgo de personalidad estable sino como las diferencias que se muestran en su percepción de los riesgos y de los beneficios de una situación determinada en un momento concreto. Por ejemplo, los estudiantes de países occidentales daban mayor peso a las probabilidades de las ganancias y la percepción del riesgo disminuía a medida que mejoraban los resultados en el juego, mientras que los estudiantes orientales concedían mayor peso en la magnitud de las pérdidas y la influencia de los resultados positivos era mucho menor en su percepción del riesgo.
Figner y Weber (2011) señalan que la idea de riesgos en la toma de decisiones depende de factores que se agrupan en términos como quién, dónde y las diferentes interacciones entre ambos. Cada individuo tiene un nivel óptimo de tensión entre la ganancia que desea obtener y la presión de riesgo que puede soportar. Según Coombs y Huang (1970), un nivel de tensión entre codicia y el miedo, donde existe un umbral de aceptación de la alternativa en ambas dimensiones donde no se elegirá una alternativa cuya ganancia sea menor que su umbral de ganancias, ni la que el riesgo sobrepasa el umbral de riesgo establecido. Para ser aceptable la alternativa no debe violar ninguno de los dos umbrales. Son reglas dentro de las estrategias de decisión no compensatorias. Así ninguno de los dos criterios puede contrarrestar al otro: un riesgo alto no compensa una gran ganancia y un riesgo muy pequeño tampoco compensaría una ganancia pequeña.
LOS HEURÍSTICOS PARA LA ELECCIÓN ENTRE ALTERNATIVAS
Aspectos básicos del enfoque del procesamiento de la información
El enfoque del procesamiento de la información se apoya en el concepto de “racionalidad restringida” propuesto por Simon (1983), quien postula que las limitaciones cognitivas conducen a la elaboración de modelos simplificados de los problemas y a tomar decisiones que sean coherentes con dichos modelos. Al simplificar la tarea de elección, se sustituye el principio de maximización por el principio de satisfacción. Por ejemplo, una persona que se plantea comprar una vivienda y tiene mucha información sobre el mercado inmobiliario, no tiene recursos de procesamiento suficientes como para poder maximizar su utilidad esperada. Para tomar la decisión tendrá que seleccionar previamente un conjunto limitado de casas para luego compararlas hasta elegir aquella que mejor se ajuste a sus aspiraciones. Este enfoque trata de sustituir el concepto de una persona racional que cuenta con toda la información, con preferencias estables y una capacidad de cómputo ilimitada por el concepto de una personal racional, pero con limitaciones en el procesamiento de la información, tales como capacidad de memoria limitada, recursos atencionales escasos, etc. Además, se debe reflejar la intersección entre estas limitaciones y las demandas impuestas por los diferentes ambientes en los que se toma una decisión. También hay que considerar el hecho de que lo que cada persona evalúe satisfactorio pueda cambiar con el tiempo y la experiencia a medida que el nivel de aspiración cambie (suele suceder con los tatuajes).
El objetivo de este enfoque consiste en describir los distintos procedimientos mediante los cuales las personas toman sus decisiones. Se requieren procedimientos heurísticos sencillos que permitan seleccionar y procesar. Ahora la elección no se basa en un análisis exhaustivo de todas las alternativas hasta encontrar la óptima sino la satisfactoria.
Payne, Bettman y Johnson (1992), señalan que las personas tienen más de una estrategia de elección y éstas pueden ser en algunas ocasiones deliberadas, otras veces, el resultado de aprendizajes previos y en otras pueden ser intuitivas. La interacción ocasiona que el conjunto de estrategias para la elección comprenda un abanico amplio de heurísticos, desde los rápidos y apropiados para las decisiones bajo presión de tiempo y poca capacidad de cómputo, hasta los de procesamiento secuencial lento y apropiado para decisiones más complejas y deliberadas.
La metodología utilizada en los estudios tratará de identificar el proceso para luego describirlo. Por ello, algunos de los métodos que se utilizan, denominados métodos para el rastreo del proceso tratan de observar directamente la estrategia empleada mediante el análisis de los protocolos verbales, el análisis de los movimientos oculares, la monitorización de la búsqueda de información y el análisis de la actividad cerebral mediante técnicas como la resonancia magnética funcional (Payne y Venkatraman, 2011). En otros casos se infiere dicha estrategia a partir de estudios en los que se presentan pares de alternativas (X, Y) de forma que si el sujeto está usando una regla determinada elegirá X y si usa otra regla llegará a la respuesta Y. Con estas técnicas tratan de cubrirse dos objetivos fundamentalmente: en primer lugar, descubrir qué estrategias y reglas elementales emplean los sujetos y, en segundo lugar, qué rasgos de la tarea y del contexto determinan la selección y uso de estas estrategias.
Criterios de elección bajo incertidumbre
Las situaciones de incertidumbre son las que mejor se ajustan a la toma de decisiones de la vida cotidiana y las situaciones de riesgo caracterizan mejor la toma de decisiones en los juegos de azar y en los ámbitos profesionales. También los criterios de elección son conocidos como reglas de decisión, heurísticos de elección, estrategias de decisión y estrategias de procesamiento de información.
Criterios de elección entre alternativas
- CRITERIO ADITIVO LINEAL. Se ajusta al modelo normativo. Se asigna a los atributos una ponderación por importancia para luego multiplicarlos por el valor determinado de ese atributo. Por ejemplo, en la compra de la casa asignamos un 9 (escala de 0 a 10) al atributo precio. A continuación, se analizará cada alternativa asignándole una ponderación al valor concreto del atributo. A una vivienda con precio medio asignamos un 5, y se multiplica por 9 (45), se suma el resultado obtenido en cada uno de los atributos para cada alternativa y se elige la de mayor puntuación. La estrategia maneja toda la información disponible y es una estrategia compensatoria porque la alternativa que tenga puntuación baja en un atributo puede compensarse con otra alta en otro.
- CRITERIO DE LA “RAZÓN INSUFICIENTE” DEL LAPLACE. Se intenta paliar la poca información en situaciones bajo incertidumbre para hacer estimaciones según modelo normativo. Se desconoce la probabilidad de resultados y se asume su equiprobabilidad. La probabilidad de todos los resultados (n) es la misma (1/n) y una vez calculado se elige la alternativa con mayor utilidad esperada.
- CRITERIO DE DOMINANCIA. Criterio coherente con modelo normativo, pero sólo para aquellas decisiones en las que exista la mejor o peor alternativa. Se exploran todas para encontrar la mejor y elegirla o la peor y eliminarla. Generalmente resulta difícil, pero es un criterio útil para un análisis preliminar con el fin de discriminar las más débiles (dominadas) y reducir el número de ellas a considerar.
- CRITERIO “EL MÁXIMO DE LOS MÁXIMOS” (MAXIMAX). Es el enfoque optimista y consiste en elegir aquella que presenta el mejor resultado considerando que éste ocurrirá (máximo de los máximos). Si son utilidades, se elige la de mayor utilidad y si son costes, la que presente el coste más bajo.
- CRITERIO “EL MÁXIMO DE LOS MÍNIMOS” (MAXIMIN). Enfoque pesimista o conservador. Se comparan los peores resultados de c/alternativa y se elige el que ofrezca el mejor de los peores resultados (máximos de los mínimos). Se toma pensando que el peor ocurrirá y pretende asegurar una ganancia mínima con el menor perjuicio.
- CRITERIO DE HURWICZ. Ni todos somos optimistas ni pesimistas, Hurwicz describió el comportamiento intermedio como la suma ponderada de los extremos: H= ? (peor resultado) + (1- ?) (mejor resultado). Se estima la probabilidad subjetiva del peor resultado y la subjetiva del mejor. La elección de este valor ? (0? ? ? 1) determina el grado de pesimismo u optimismo de la persona. Si a fuera igual a 1, entonces sería pesimista (maximín) y si a fuera igual a 0 sería optimista (maximax).
- CRITERIO DE LA PÉRDIDA DE OPORTUNIDAD DE SAVAGE (NINIMAX). También conocido como arrepentimiento porque considera que las personas también lamentan no haber escogido una alternativa. Se busca reducir el arrepentimiento al mínimo. Se elige el mejor resultado y se sustituye por cero (0) Este representa que no hay arrepentimiento. Luego se encuentra la diferencia entre el resultado óptimo y los demás. Esta diferencia representa la pérdida de oportunidad o arrepentimiento por no haber escogido la alternativa que diera el mejor resultado y se elige la que presente el mínimo arrepentimiento.
- CRITERIO DE SATISFACCIÓN CONJUNTIVA. Este criterio es semejante al general de satisfacción propuesto por Simon. Se establece una línea de corte o umbral para cada uno de los atributos y se elige la que alcance este nivel de satisfacción en todos los atributos. Se utiliza para el análisis preliminar de un conjunto amplio de alternativas con el fin de seleccionar el subconjunto de las mejores o para elegir la alternativa satisfactoria.
- CRITERIO DE SATISFACCIÓN DISYUNTIVA. Semejante al anterior, pero se eligen las alternativas que alcancen el nivel de umbral de satisfacción en cualquiera de los atributos, no en todos (alternativa destacada en al menos un atributo).
- CRITERIO DE RECONOCIMIENTO. Existe tan poca información sobre las alternativas que se eligen las que reconocen o que les resulta familiar. Forma parte de las estrategias heurísticas “rápidas y frugales” porque requieren poco esfuerzo cognitivo en términos de recursos y tiempo.
Criterios de elección entre atributos de las alternativas
Los criterios para la elección interalternativas son en los que se compara el valor de cada una de las consecuencias o atributos de todas las alternativas:
- CRITERIO DE LA DIFERENCIA ADITIVA. Se ajusta al modelo normativo. Va comparando cada uno de los atributos en un par de alternativas Se asignan todos los valores a los atributos ponderados por su importancia y se compara un par de alternativas, luego se suman las diferencias entre ellos y se elige la alternativa superior. Posteriormente se compara ésta con otra y se vuelve a proceder hasta que solo quede una. Toma toda la información disponible y es compensatorio.
- CRITERIO LEXICOGRÁFICO. Se determina primero cuál es el atributo más importante y luego se elige la alternativa que presente el valor más alto en dicho atributo. Se denomina lexicográfico porque los atributos se ordenan en función de la importancia de forma análoga a cómo están ordenadas alfabéticamente las palabras en un diccionario. Es de los criterios más comunes.
- CRITERIO DE LA ELIMINACIÓN POR ASPECTOS (Tversky, 1972). Similar al anterior, pero establece líneas de corte para el valor de cada atributo. Se empieza por determinar el más importante y su nivel de satisfacción y se eliminan todas las alternativas que no llegan a él. Se continúa con el siguiente sucesivamente. P. ej., Elegir restaurante cerca de casa. Podemos elegir como primer atributo que tenga cocina tradicional y como línea de corte, que tenga buen pescado. La línea de corte eliminará cualquier restaurante que no cocine pescado. El segundo atributo puede ser el rango de los precios, eliminando los que tengan precios más altos que los aceptables. Otro el tipo de local que nos guste y así hasta que nos quede solo una opción.
- CRITERIO DE LA RAZÓN ÚNICA (Gigerenzer y Todd; 1999; Gigerenzer y Selten, 2002). La decisión se toma basándose en un único atributo y forma parte de los heurísticos “rápidos y frugales” Similar al lexicográfico, pero con dos heurísticos de búsqueda para la selección del primer atributo:
- El heurístico “escoge el mejor”, lo escoge por la validez que haya tenido en experiencias anteriores para la discriminación entre buenas y malas y los ordena de mayor a menor validez.
- El heurístico “minimalista” realiza la comparación entre atributos de forma aleatoria hasta encontrar la alternativa con el atributo de mayor validez.
Los criterios de decisión que acabamos de ver también se clasifican como estrategias compensatorias, dado que una puntuación alta en un atributo puede equilibrar una baja puntuación en otro, y estrategias no compensatorias porque no se permiten intercambios entre las puntuaciones de los atributos. Las reglas compensatorias son más completas porque tienen en cuenta todos los atributos y las posibles relaciones entre los mismos, como al adquirir una vivienda que un precio alto, puede compensarse por la cercanía al puesto de trabajo. Sin embargo, estas compensatorias y coherentes con el modelo normativo son costosas cognitivamente y poco viables para decisiones con muchas alternativas multiatributo.
Elegir una u otra estrategias dependerá:
- Del análisis de la relación entre el coste de optimizar el proceso y el beneficio de simplificarlo.
- De factores contextuales y del entorno de la tarea.
- De la representación del problema.
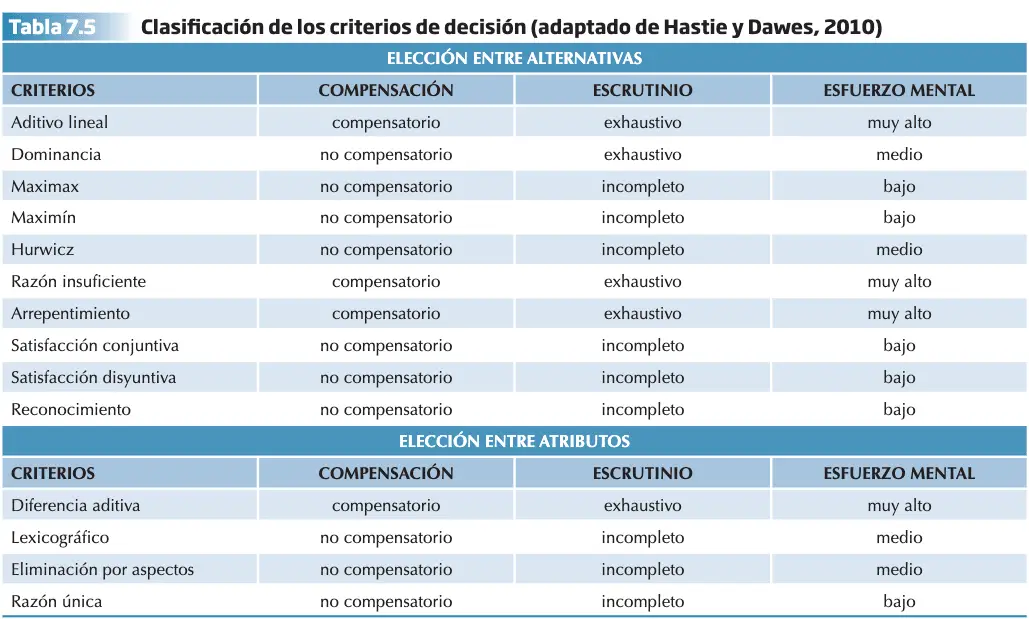
Algunas variables como la presión del tiempo, información distractora, dificultad de la tarea influyen en el uso de la estrategia y por tanto en las distintas respuestas. En diferentes investigaciones, se observa que las personas modifican la estrategia empleada cambiando a más simples centradas en los datos negativos que permiten la eliminación de ciertas alternativas. Se observa también el proceso de cadenas de estrategias o reglas, de forma que primero se usan las que permitan descartar y luego se evalúa más detalladamente. Parecen útiles en diferente contexto, pero no se puede olvidar que el descarte inicial puede llevar a despreciar alternativas atractivas.
ALGUNOS ASPECTOS COLATERALES DE LA TOMA DE DECISIONES
Uno de los aspectos que acompañan a la toma de decisiones es la necesidad de justificación de la respuesta emitida. Según Shafir, Simonson y Tversky (1993) el análisis de las razones por las cuales se toma una decisión permite una mejor aproximación a los aspectos psicológicos de este proceso y puede arrojar luz a la inconsistencia de los modelos normativos.
Esta necesidad de justificar está relacionada con el fenómeno estudiado por Festinger (1964) sobre la necesidad de reducir la disonancia cognitiva. Las personas suelen estar satisfechas de sus decisiones porque no conocen el resultado obtenido en caso de haber elegido otros, y por la tendencia a eliminar la disonancia. Desde una perspectiva teórica más comprensiva, Svenson (1996) considera que la toma de decisiones es en gran medida el arte de resolver conflictos por medio de la reconciliación o negación entre metas contradictorias, siendo esta resolución además dependiente del problema, el contexto y las diferencias individuales. Se ha de tener en cuenta que la decisión no es un proceso estático, sino que debe reconsiderarse repetidamente a medida que surgen otros elementos o varían las condiciones. Nuestros valores o utilidades son inestables, muchas veces por desconocimiento. Es preciso tener en cuenta el cono- cimiento de la persona experta frente a la ingenua. Además, cada uno lleva a cabo varios roles en la vida y cada uno de éstos determina una perspectiva diferente que variará la utilidad para cada dimensión. El estado anímico dará lugar a juicios más positivos o negativos, modificando las decisiones. El más positivo dará lugar a búsqueda de alternativas variadas y a la sobrevaloración de la ocurrencia de estados favorables, y a la inversa.
A veces las decisiones están “cargadas” emocionalmente. Algunas personas no pueden considerar detalles monetarios a la posibilidad de salvar vidas o salvaguardar el medio ambiente. Tetlock (2002) las considera como compensaciones tabú, puesto que hay una resistencia a enfrentar lo sagrado y lo profano. Pueden ante esto negarse a decidir, dejar que otros lo hagan por ellos, optar por alternativa que mantenga el estatus quo o que puede justificar fácilmente ante ellos y los demás, utilizando estrategias no compensatorias; o bien intentar abordar el tema con esfuerzo de recursos y tiempo ponderando aspectos emocionales como importantes.
Payne y Bettman (2004), señalan que las ventajas y desventajas de las decisiones, se encuentran directamente relacionadas con los siguientes objetivos:
- Maximizar la precisión de la decisión.
- Minimizar el esfuerzo cognitivo.
- Minimizar el impacto de las emociones negativas durante el proceso y una vez tomada.
- Maximizar la facilidad con la que se pueda justificar la decisión.
ESQUEMA

REFERENCIAS
•RESUMEN M. GORETTI GONZÁLEZ
•GONZÁLEZ LABRA, M., SÁNCHEZ BALMASEDA, P., & ORENES CASANOVA, I. (2019). PSICOLOGÍA DEL PENSAMIENTO. MADRID: SANZ Y TORRES.


